Locality Sensitive Hashing
Contents
Locality Sensitive Hashing¶
Finding Nearest Points: Given a set of data points and a query data point, we have to find the data point closest to this query point. We also have to find the K-nearest neighbours or some set of points which satisfy the condition
\(d(p,query) < r\), where r is some given distance.
This point may be a representation of a multiset or a vector which represents a document.
If we are taking the datapoints as a part of a document, the near points represent similarity within a document.
The words in the documents need to be represented in some mathematical entity.
Representation of a document as Sets¶
Any document is represented by the words it contains. The words may be represented by their position on the document, but the spatial orientation of the words is not a very useful attribute of the representation.
Thus the document is represented by the set of words it consists.
Separation of the elements in the set¶
Natural separators are not always reliable for a document. Thus a document is separated into Shingles.
Shingles are a set of k consecutive characters that make up the entire document. These Shingles are often hashed to 64bit numbers for each of storage.
A document = Set of Shingles
Example: A Sly fox jumped
\(k=5\)
Shingles:
a sly
sly f
ly fo
.
.
.
Shingles are more appropriate method of separation because, they represent and preserve the semantics of a document. Most of the time, while comparing the document, we have to take into account the semantic similarity.
Measure of Similarity¶
Jaccard Similarity \(JS(A,B) = \frac {|A \cap B|} {|A \cup B|}\)
\(JS(A,B) \in [0,1]\)
Jaccard Distcance : \(JD(A,B) = 1 - JS(A,B)\)
\(JD(A,B) \in [0,1]\)
Jaccard Distance is a metric property. It satisfies the following :
1.
\(JD(A,A) = 1- \frac {|A \cap A|} {|A \cup A|}\)
\(JD(A,A) = 1- 1\)
\(JD(A,A) = 0\)
\(JD(A,B) = 1- \frac {|A \cap B|} {|A \cup B|}\)
\(JD(A,B) = 1- \frac {|B \cap A|} {|B \cup A|}\)
\(JD(A,B) = 1-JS(B,A)\)
\(JD(A,B) = JD(B,A)\)
Jaccard Distance is symmetric
JD(x,y) can only lie between 0 and 1. Thus \(JD(A,B) \ge 0\)
\(JD(A,C) < JD(A,B) + JD(A,C)\)
Triangle inequality is also satisfied by Jaccard distance.
Representation of Documents as Vector¶
Vectors can be used in various instances for representation. They can be used to represent an image (over 64x64 or 128x128 domains) or the spatial distribution of data. Their use can also be extended to documents
In Documents, the vector representation is similar to that of sets. Each vector direction represents the position of a shingle in the document and the magnitude can be related to the weightage of the shingle.
Similarity between Documents¶
Given any Document, if we pass the shingles through a hash function and compare the hash values, we can get the values where shingles are exactly same. But there is no way we can say that two shingles are similar through the same approach.
Example:
x= acted , y= acted , z= acced
The Hash function would easily detect that x and y are exact but not detect that x and z are 80 % similar
Locality Sensitive property¶
The exact equality of the two shingles are detected because they are assigned to the same index by the hash function. Taking this idea, Indyk Motwani repuroposed the occurance of collisions in the hash functions, i.e., if two entities x and y are similar, they collide (same value is produced by the hash function) and not if they are vastly different.
Relating to our earlier problem of finding nearest points. If two points in a space are nearby, the chances of collision is high.
\(Pr[h(x)=h(y)] \) is high if x and y are close
\(Pr[h(x)=h(y)] \) is low if x and y are far apart
Such kind of function will solve both the problems, however no such clear function exists. To slove such problems, a hash family is designed, given the distance function or similarity function.
At runtine, a single hash function is chosen from this family to calculate the similarity.
This function is then called Locality sensitive if the above two probabilities is satisfied.
In Terms of similarity function, given a universe U, and siilarity s:U x U -> [0,1], does there exist a probability distribution over some hash family H such that
\(Pr[h(x)=h(y)] = S(x,y)\)
\(S(x,y) =1 \Rightarrow x=y\)
\(S(x,y) = S(x,y)\)
Hamming Distance¶
Used when the points are denoted by a bit string of fixed and equal length.
point \(\to\) bit string of length d.
H(x,y) = {i, \(x_{i} \neq y_{i}\)}
\(S_{H}(x,y) = 1-\frac {H(x,y)} {d}\)
For Example: x=1011010001, y= 0111010101
d=10
number of dissimilarities H(x,y) =3
S(x,y) = 1-3/10 =0.7
Locality Sensitive function for this distance?¶
In order to create a LSH for such a problem, the hash family must be sampling a set of positions. Let the be a hash family such that
H ={\(h_{i}(x)=x_{i} | i=1,2... d\)}
|H| = d
From this family H, a function h is chosen randomy to achieve the probability of similarity.
\(Pr_{h\in H}[h(x)=h(y)] = S(x,y)\)
If we extend the dame function to k coordinates instead of 1, we get a more precise equation. In the above example itself, let S={1,5,7}
Existence of Locality Sensitive Hashing¶
Since we are choosing k-coordinates, where k = |S| and we know that for a single coordinate:
Pr[h(x) = h(y)] = 1 - \(\frac{H(x,y)} {d} = S_{h}(x,y)\)
The Probability for k coordinates:
Pr[h(x) = h(y)] = \((1 - \frac{H(x,y} {d})^{k} = (S_{H}(x,y))^{k}\)
Locality Sensitive Hashing for Angle Distance¶
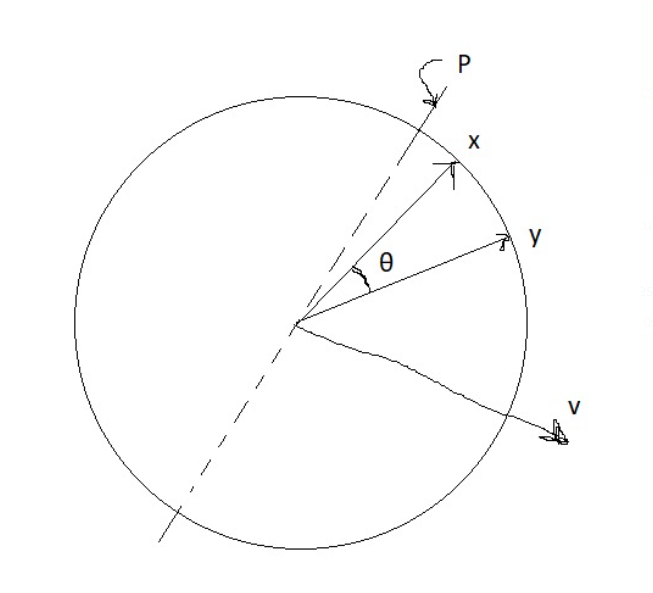
Let x and y be unit normal vectors, i.e. radii in a circle of radius 1.
Therefore, |x| = |y| = 1
x,y = |x||y|cos\(θ\)
\(⇒\) x.y = cos\(θ\)
\(\theta = cos^{-1}(x.y) = d(x,y)\) [angle distance]
Since, the total angular distance in a circle is [-x,x]
S(x,y) = 1 - \(\frac {\theta} {x} \in\) [0,1]
Corresponding notion of local sensitivity hashing:
Choose a normal vector v at random
Now, \(h_{v}\)(x) = sign(v.x) = \(±1\) (or ‘1’ and ‘0’ in binary)
Let P be a hyperplane \(\perp\) to v
Then, the half containing \(\vec{v}\) yields +1 and the other half yields -1
Pr[h(x) = h(y)] = 1 - \(\frac {\theta} {x}\)
The hyperplane gives different signs for x and y if it passes through \(\theta\) with probability \(\frac {\theta} {x}\)
Thus the probability of x and y giving some signs is 1 - \(\frac {\theta} {x}\)
Aside : Picking a direction u.a.r
Picking a vector in d-dimensions (x \(\in\) R\(^d\)) such that norm of x = 1 (|x|\(_{2}\) = 1) and, the direction is uniform along all possible directions
Take the Gaussian distribution and generate d independent samples.
x = (\(x_{1},x_{2}, ..... x_{d}) \thicksim N(0,1)\)
Normalize it with the length of the vector \((\frac {x} {|x|_{2}})\)
L\(_{2}\) norm of x = \(\sqrt{\Sigma x_{i}^2} \)
Writing the equation in polar form gives us independent r and \(θ\). With r normalized, we are left with a uniformly chosen direction.
