Object Representations¶

Introduction¶

Data science involves using scientific tools, algorithms and data models to statistically analyse and extract knowledge from large volumes of processed/unprocessed collected data.
Mathematically, an object can be represented in 2 ways:
- Object Representation: To depict isolated objects like vectors (words in a document), sequences (DNA), etc.
- Network Representation: To show interaction among objects like graphs (friendship network, road connections), etc.
The most common representation for documents is called ‘bag of words’ representation.
- First, the document sentences are tokenized.
- Then their base forms are derived via stemming and lemmatization.
- The collected lexemes are then converted to n-gram or skip-gram models. As n increases, the size of the word dictionary and thus, the memory required to store it increases, but contextual information is captured more efficiently.

Note

It implies that as we move from unigram to bigram, the connection between mathematical similarity and intuitional similarity becomes tighter.

Distance Functions¶

Distance is a measure of similarity between objects. It is desirable (useful in divergence functions and clustering algorithms) that these functions (\(d\)) have the following properties:

\(d(x,x)=0, d(x,y) \ge 0\)
\(d(x,y) = d(y,x)\)
\(d(x,y) + d(y,z) \ge d(x,z)\) (Triangle Inequality)

A function satisfying these properties implies:

\[ d(x,y) = 0 => x = y \]

It is further useful to have a simple calculation for a point \(x\) that gives the least sum over distances with other points \(p\) in space.

\[ \min\limits_{x} \sum_{i} d(p_i,x) \]

1. \(L_p\) Norm¶

The \(l_p\) norm between two \(d\) dimensional objects (like vectors) \(x\),\(y\) can be computed as follows:

\[ L_p(x,y) = (\sum_{i=1}^{d} |x_i - y_i|^{p})^{1/p} \]

It satisfies all the aforementioned metric properties.

A. \(L_1\) norm

\[ L_1(x,y) = |x_1-y_1| + |x_2-y_2| + ... |x_d-y_d| \]

For one-dimensional points, \(\min\limits_{x} {\sum_{i}} d(p_i,x)\) occurs at the median of the points lying on the line.

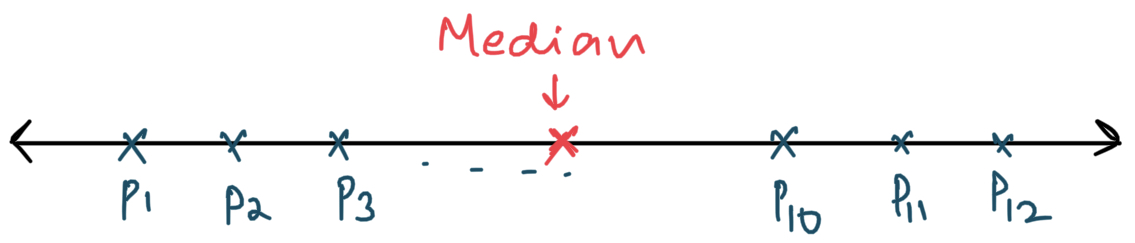
Fig. 3 ‘Centre’ of \(L_1\) norm is the median.¶

B. \(L_2\) norm

\[ L_2(x,y) = |x_1-y_1|^{2} + |x_2-y_2|^{2} + ... |x_d-y_d|^{2} \]

The \(d\) dimensional point \(x\) such that its sum of distances from other \(d\) dimensional points \({p_1, p_2, ... p_n}\) is minimum can be computed as follows for each dimension:

\[ \min\limits_{x} \sum_{i=1}^{n} |p_i-x|^{2} => \frac{\partial \sum_{i=1}^{n} |p_i-x|^{2} }{\partial x} = 0 \]

\[ \sum_{i=1}^{n} 2(p_i - x) = 0 \]

\[ x = \frac{\sum_{i=1}^{n} p_i}{n} \]

C. \(L_\infty\) norm

Let \(S_i\) = \(|x_i - y_i|\). We define the \(L_\infty\) norm as,

\[ L_\infty(x,y) = \lim_{p \to \infty} (\sum_{i=1}^{d} S_i^{p})^{1/p} \]

Let \(S_1\) be the maximum distance between two coordinates of \(x\) and \(y\) i.e. \(S_i < S_1 \forall \:i\).

\[ \lim_{p \to \infty}(|S_1|^{p}\sum_{i=1}^{d} (\frac{S_i}{S_1})^{p})^{1/p} \]

\[ S_1\lim_{p \to \infty}(1+\sum_{i=2}^{d} (\frac{S_i}{S_1})^{p})^{1/p} ≈ S_1 \]

2. Jaccard Distance¶

Jaccard Distance (\(JD\)) is a distance function used to measure dissimilarity between sets. Other distance functions like Euclidean distance can not be used for sets. This is because if the two words are very similar, then their embedding representations are bound to be very similar and in some cases, sparse. Using Euclidean distance on high dimensional vectors and sets is computationally expensive and may not yield the correct result.

Consider two sets \(A\) and \(B\) in space \(S\). The Jaccard Similarity \(JS(A, B)\) is defined as,

\[ JS(A,B) = \frac{|A\cap B|}{|A\cup B|} \]

If the two sets are mutually exclusive, \(|A\cap B|=0\). Hence, \(JS(A,B)=0\). Similarly, if \(A=B\), \(JS(A,B)=1\)

The Jaccard Distance (\(JD\)) between 2 sets \(A,B\) is given as,

\[ JD(A,B)=1-JS(A,B) \]

This implies, \(A=B \iff JD(A,B)=0\)

Additionally Jaccard Distance follows all the three metrics of a distance function, even the triangle inequality rule.

3. Edit Distance¶

Edit Distance is defined as the minimum number of specific kinds of operations (each with a mentioned cost) required to modify an object of a class to another object of the same class. The objective is to minimise the cost associated with edit distance while modifying an entity. The higher the edit distance, the higher is the difference between the entities.

The permissible operations for strings \(A\) and \(B\) are:

Insertion (cost=1): Adding a character in \(A\) at the desired position \(i\) so that the character at position \(i\) of \(A\) and \(B\) match. Consider strings \(A\) = ‘sittig’ and \(B\) = ‘sitting’. We can insert an ‘n’ at the 6th position to match the characters at that position.
Deletion (cost=1): Removing a character in \(A\) at the desired position \(i\) so that the character at position \(i\) of \(A\) and \(B\) match. Consider strings \(A\) = ‘brack’ and \(B\) = ‘back’. We can delete the ‘r’ at the 2nd position to match the character ‘a’ at the 2nd position of \(A\) and \(B\).
Substitution (cost=1): Replacing a character in \(A\) at the desired position \(i\) so that the character at position \(i\) of \(A\) and \(B\) match. Consider strings \(A\) = ‘herlo’ and \(B\) = ‘hello’. We can substitute the ‘r’ at the 3rd position with an ‘l’ to match the characters at that position.

Edit Distance for two strings \(A\) and \(B\) is the minimum cost of the mentioned operations to convert \(A\) into \(B\) or vice-versa.

Similar to \(L_p\) norm and Jaccard Distance, Edit Distance obeys all three mentioned metrics of distance functions. Let \(d(x,y)\) be the edit distance (or minimum cost of operations) for two strings \(x\) and \(y\); defined as the cost to modify \(x\) to \(y\).

a) \(d(x,x)=0\)
This is trivial as the minimum number of operations (and cost) to change string \(x\) to \(x\) is 0.
b) \(d(x,y)>0 \iff x\neq y\)
If \(x\) is not equal to \(y\), there will be atleast one operation with an associated cost \(c_i\) required to change or modify \(x\) to \(y\).
\(d(x,y)=d(y,x)\)
Consider the cost required to update \(x\) to \(y\) (or edit distance of \(x,y\)) is \(c\). We can argue that the minimum cost required to update \(y\) to \(x\) is \(c\) by replacing insertion with deletion, deletion with insertion for \(d(y,x)\)
\(d(x,y)+d(y,z)\geq d(x,z)\)
Let \(d(x,y)=c_1\;,\; d(y,z)=c_2\). We can argue that \(d(x,y)+d(y,z)< d(x,z)\) is FALSE. This can be done by contradiction.
Let \(d(x,y)+d(y,z)< d(x,z)\) with \(\;d(x,y)=c_1\;,\; d(y,z)=c_2\)
Or, \(\;c_1+c_2< d(x,z)\)
However, we can easily argue that we can update \(x\) to \(z\) by updating \(x\) to \(y\) and then updating \(y\) to \(z\). Since edit distance gives the minimum number of operations associated with the cost, \(d(x,z)\) can be \(c_1+c_2\) at max. Therefore, our assumption is wrong.
Hence, \(\;d(x,y)+d(y,z)\geq d(x,z)\)

CS328-2022 Notes

Object Representations

Contents