.ipynb .pdf

repository open issue suggest edit

Contents

Relation between second eigenvalue of Laplacian and Spectral Clustering

---

\( \rightarrow \) If \( \phi^* \) is conductance of \( G, \) we can use \( v_2(L) \) to find a cut of conductance

\( O(\sqrt{\phi^*} logn) \)

\( \rightarrow \) For any vector \( v, \)

\( v^TLv = \sum_{ij \in E} (v_i - v_j)^2 \)
\( L = D - A \)
\( v^TLv = v^TDv - v^TAv = \sum_{i=1}^n d_iv_i^2 - \sum_{i}v_i \sum_{j}A_{ij}v_j \)

\( LHS = \sum{div_i^2} - \sum_{ij}{v_i v_j A_{ij}} = \sum{d_iv_i^2} - 2\sum_{ij \in E}{v_iv_j} \)
\( RHS = \sum_{ij \in E}{(v_i - v_j)^2} = \sum{d_iv_i^2} - 2\sum_{ij \in E}{v_iv_j} \)

\( \rightarrow \) We saw that \( v_1 = \bar{1} \frac{1}{\sqrt{n}} \)

\( \lambda_2 = \min_{v \perp \bar{1}, v \neq 0} \frac{v^TLv}{d(v^Tv)} = \min_{v \perp \bar{1}, v \neq 0} \frac{\sum_{ij \in E}{(v_i - v_j)^2}}{d \sum_{i}{v_i^2}} \hspace{20mm}(1) \)

where

\( \bar{1} =\begin{bmatrix} 1 \\ 1 \\ 1 \\ . \\ . \\ 1 \end{bmatrix} \)

\( \underline{Claim:} \) We can also write

\( \lambda_2 = \min_{u, u \neq 0} \frac{\sum_{ij \in E}{(u_i - u_j)^2}}{\frac{d}{n} \sum_{\{ ij \}}{(u_i - u_j) ^ 2}} \hspace{20mm}(2) \)

Consider a set \( S \subseteq V \)

\( S_{i} = \begin{cases} +1, i \in S\\ 0, i \notin S \end{cases} \)

\( \sum_{ij \in E}{(S_i - S_j)^2} = e(S, \bar{S}) \)

\( Denominator = \frac{d}{n} |S||\bar{S}| \)
\( R(S) = \phi(S) \)

where

\( R(S) = \frac{\sum_{ij \in E}{(v_i - v_j)^2}}{\frac{d}{n} \sum_{\{ ij \}}{(v_i - v_j) ^ 2}} \)

\( \rightarrow \) If \( u \perp \bar{1}, \) then denominator of \( (2) \)

\( = \frac{d}{n} \sum_{\{ i,j \}}{(u_i - u_j)^2} = \frac{d}{2n} \sum_{ij}{(u_i - u_j)^2} \)
\( = \frac{d}{2n} (n \sum_{i}{u_i^2} + n \sum_{j}{u_j^2} - 2 \sum_{ij}{u_iu_j}) \)
\( = \frac{d}{2} \times 2 \sum{u_i^2} - \frac{d}{2n} \times 2(\sum{u_i})^2 \)
\( = d \sum{u_i^2} = \text{Denominator of } (1) \)

\( \rightarrow \) Rayleight quotient for \( S \)

\( R(S) = \frac{e(S, \bar{S})}{|S| |\bar{S}| \frac{d}{n}} = \sigma(S) = \sigma(G) \text{ if S = optional set for } \sigma(S) \)
\( \lambda_2 \leq \sigma(G) \leq 2\phi(G) \)

Hence \( \lambda_2 \) is really a “relaxed”/soft version of \( \sigma(G) / \phi(G) \)

Cheeger’s Inequality

\( \lambda_2 \leq 2\phi(G) \)
\( \lambda_2 \geq \frac{\phi(G)^2}{2} \)

\( \hspace{3mm} \) Implies that using \( v_2, \) we can find a cut where expansion is

\( O(\sqrt{\lambda_2} logn) = O(\sqrt{\phi(G)} logn) \)

Spectral Clustering

\( \rightarrow \) For regular graphs
\( \hspace{5mm} - \) Find \( L = dI - A \) or \( I - \frac{1}{d}A \)
\( \hspace{5mm} - \) Find \( v_2(L) \)
\( \hspace{5mm} - \) Sort all vertices by their coordinates of \( v_2 \)
\( \hspace{5mm} - \) Find best prefix i.e. \( S_i = \{ 1, ..., i \} \) as per new numbering

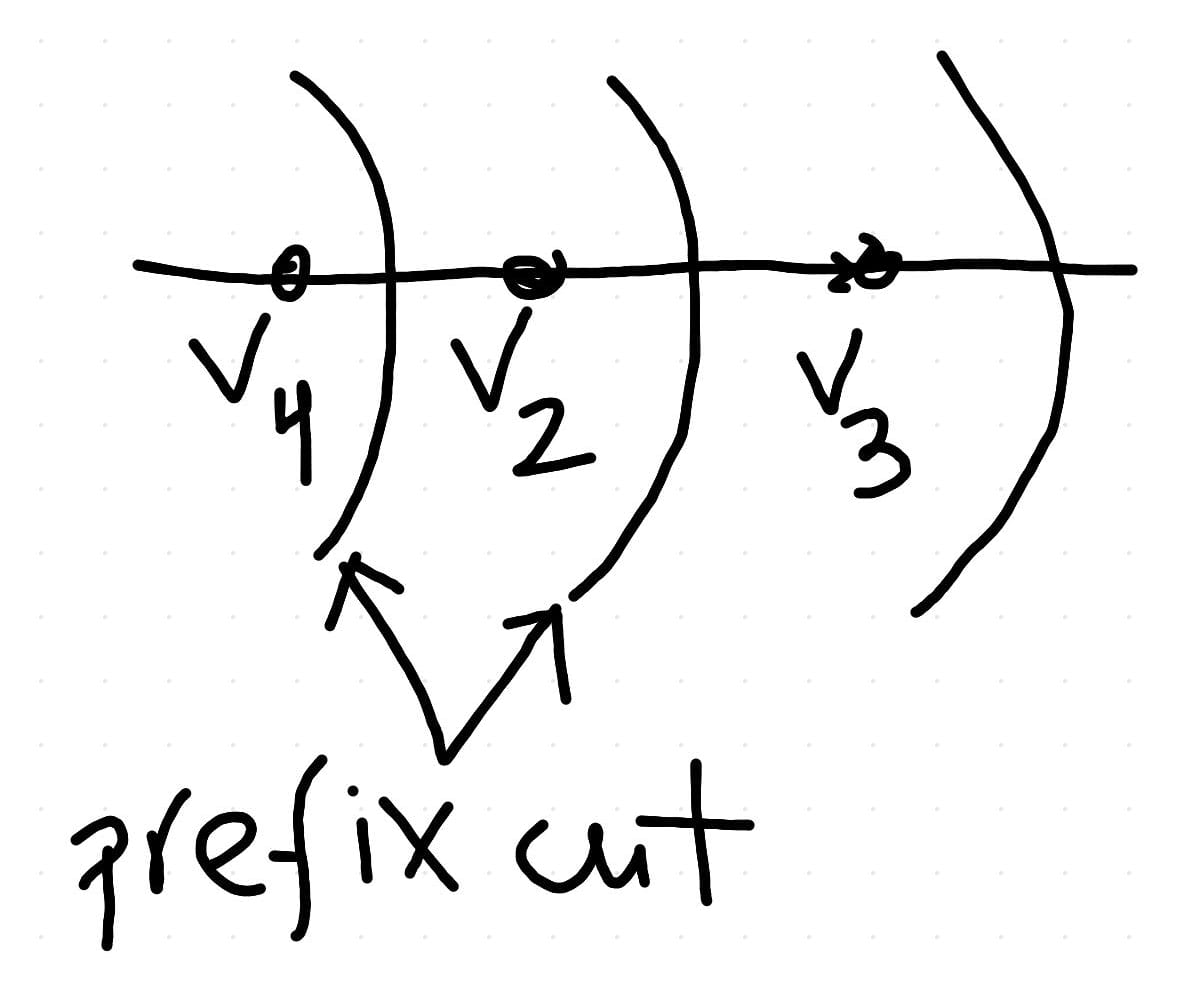
Fig. 28 Spectral Clustering

\( \\ \hspace{5mm} \) n cuts \( \rightarrow \) report one with smallest conductance

\( \rightarrow \) For non-regular graphs,
\( \hspace{5mm} - L = I - D^{-1/2}AD^{-1/2} \)
\( \hspace{5mm} - \) Calculate \( v_2(L) \) and still find best prefix cut
\( \hspace{5mm} - \) If \( \phi^* \) is optimal conductance cut, we are guaranteed a cut of conductance no more that \( O(\sqrt{\phi^*} logn) \)

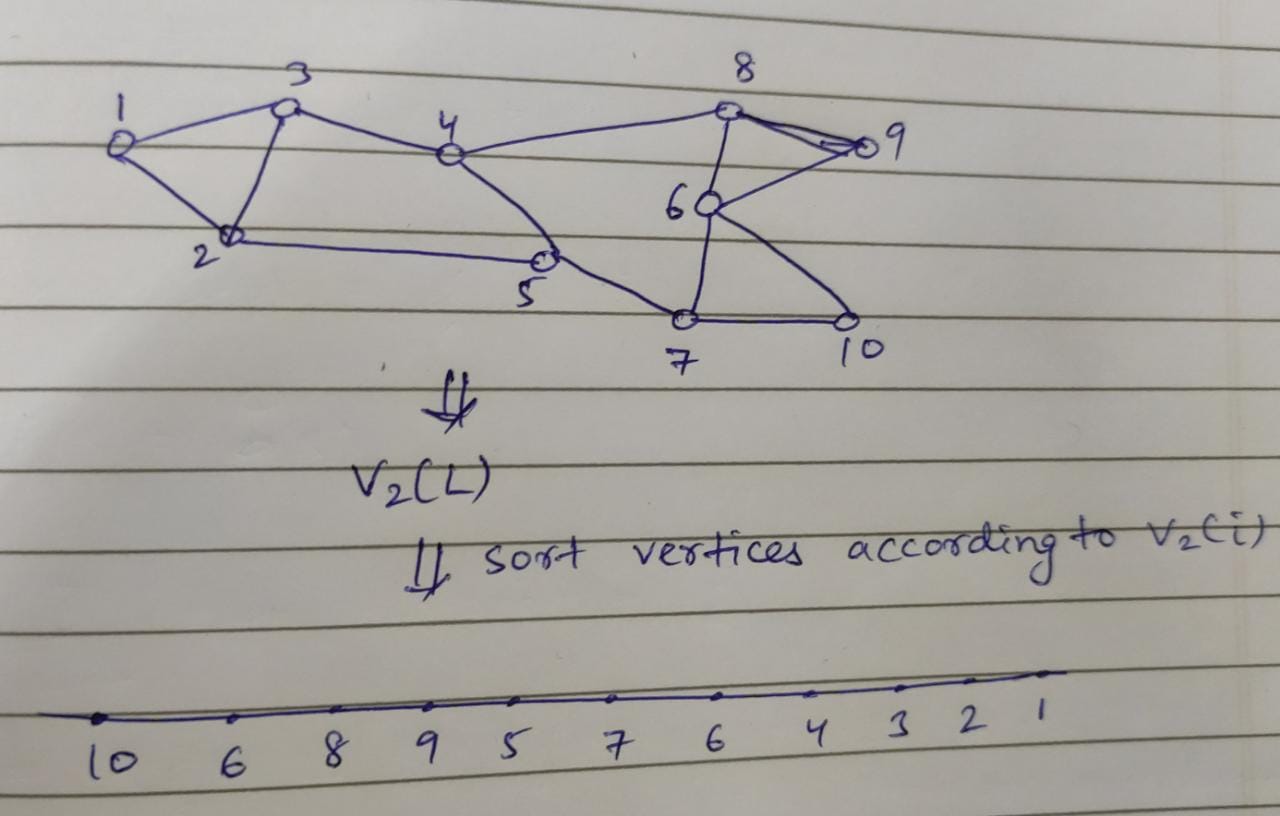
Fig. 29 Sorting of vertices in Spectral Clustering

previous

Graph Laplacian and its Eigenvalues

next

Mixture Models