Densest Subgraph
Contents
Densest Subgraph¶
Let G,S be the graph and Subgraph/Cluster defined as following:
a) The edges in the Subgraph S are denoted as e(S,S).
b) The number of nodes in S is denoted as |S|.
c)Density of Subgraph is given by Den(S) and Den(S)=\(\frac{e(S,S)}{|S|}\)
The subgraph having the maximum density will be known as Densest Subgraph.
BackGround¶
The Densest Subgraph Problem can be solved using 2 algorithms. They are
Max flow based algorithm in Directed graphs.
Flow based algorithms by Goldberg in undirected graphs.
Greedy Algorithm which gives 2-Approx algorithm in undirected and directed graphs.
We have seen flow based algorithms and Max flow/min cut based algorithms in previous notes. Let us discuss here about the Greedy Algorithm.
Greedy Algorithm¶
Introduction¶
This greedy algorithm for densest subgraPhs is given by Charikar.
Generally while building this densest subgraph using greedy algorithm, the intuition tells us to select the node having highest density and then another node with next highest density and so on. But this is not accepeted. The reason being:
The density(S)=\(\frac{e(S,S)}{|S|}\). The number of edges(#e(S,S)) would be zero when there is only one node.
Also,Even if the e(S,S) will increase with increase in nodes the number of vertices also increases.
Thus,finding the density using greedy algorithm in this way is not appreciated.
Algorithm(Psuedocode)¶
First consider all the nodes in the graph. Start with \(V_o=V(G)\)
k=|V|(number of vertices/nodes)
Following is the pseudocode for Greedy Algorithm:¶
Algorithm:
For i in range n(number of vertices)
Find \(deg_i(\nu_i)\) (Degree of every \(\nu_i \in V(G)_i\) restricted to \(V(G)_i)\)
For i =k to 2
Do: \(\nu\) be the vertex in \(V_i\) of minimum degree then
\(V_{i-1}\)=\(V_i\)-{𝜈}
\(return (V_j\),which has maximum density among \(V_i\),where i=1,2,..k)
Let us take an example. A graph has 9 vertices and connected as shown below.
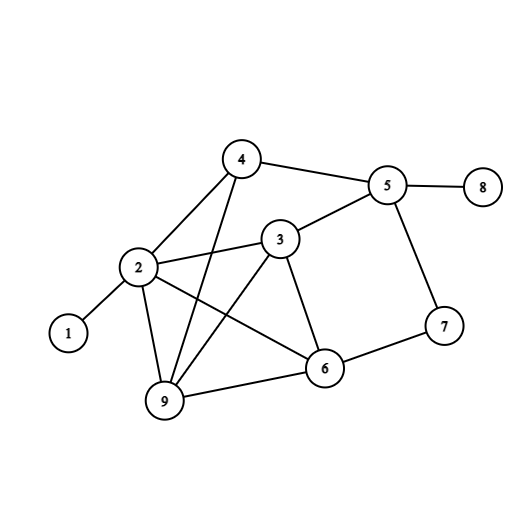
Fig. 13 Sub_graph¶
The densities of all vertices are mentioned in the table.The Densities are calculated as per the greedy algorithm discussed above.
V0 |
V1 |
V2 |
V3 |
V4 |
V5 |
V6 |
V7 |
V8 |
|---|---|---|---|---|---|---|---|---|
13/9 |
12/8 |
11/7 |
9/6 |
7/5 |
6/4 |
3/3 |
1/2 |
1/1 |
So,\(V_2\) has highest density among all nodes in the graph.Thus all nodes conneted to \(V_2\) will be the Densest Subgraph
Note
Density(Greedy algo) is bounded by Density(Opt). Density(Opt)\(\geq\)Density(Greedy)\(\geq\) \(\frac{1}{2}\)Density(Opt)
Proof:
Let \(S^{}\) be vertices of optimal subgraph. Then Den(Opt)=\(\frac{e(S^{},S^{})}{|S^{}|}\).
Claim: Any \(\nu \in S^{}\),\(deg_{S^{}}(\nu)\geq Opt.\) where \(deg_{S^{}}(\nu)\) is degree of \(\nu\) in \(S^{*}\)
Consider \(S^{}\) and \(S^{}\)-\({\nu}\)
By the definition of optimum,we can say that
Now,Let us say that for the first a vertex \(\nu\) has been removed from \(S^{*} \) Let S be the current set of vertices before removing \(\nu\).
So, we can say \(deg_{S}u \geq \)\(deg_{S}\nu\) for all u\(\in\) S.
Divide by |S| on all sides.
Hence proved that \(Density(Opt)\geq Density(Greedy)\geq\frac{1}{2}Density(Opt)\)
Alternate definition of Graph Clustering¶
Imagine partioning solid objects, the best way of partitioing the object could be interpreted as partition at the part where surface to to the volume ratio is final.
For example: The best way of partitioning a dumbell would be breaking it in the middle of the handle.
Similar analogy can be applied to graphs also.
Expansion¶
Let us take a graph as shown below and partition them into S and \(\bar{S}\).
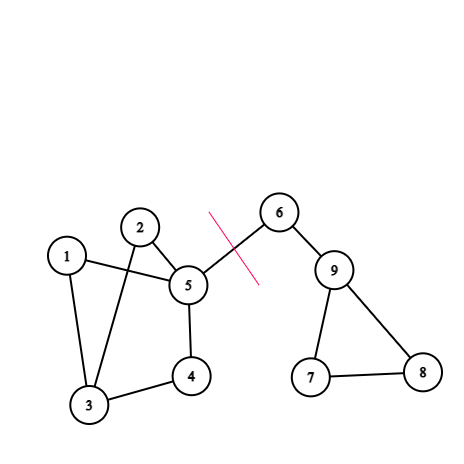
Fig. 14 Expansion_cut¶
Here, the edge 5-6 will be cut and the subgraph with node 5 is S and another part is \(\bar{S}\)
Now,expansion of the set S =\(\frac{e(S,\bar{S})}{Min(|S|,|\bar{S}|)}\)
Where \(e(S,\bar{S})\) is number os edges between S and \(\bar{S}\)
