Hierarchical Clustering¶

Why ?¶

Hierarchical Clustering can be used when we do not know the target number of clusters.
This clustering mechanism is also very useful because we can produce a family of clusters, for each k.

Note

A lot of papers have been written on hierarchial clustering. Researchers use this hierarchy to match with the natural hierarchy to obtain results. Eg :- Hierarchical clustering is used in Gene Sequencing and DNA matching etc.

Ways of doing Hierarchical Clustering:¶

Top-Down/divisive: bi-partition
Bottom up/agglomerative: aggregating from individual point

Note

Single Linkage Clustering is one of the most common heirarchical clustering. It is an example of agglomerative clustering

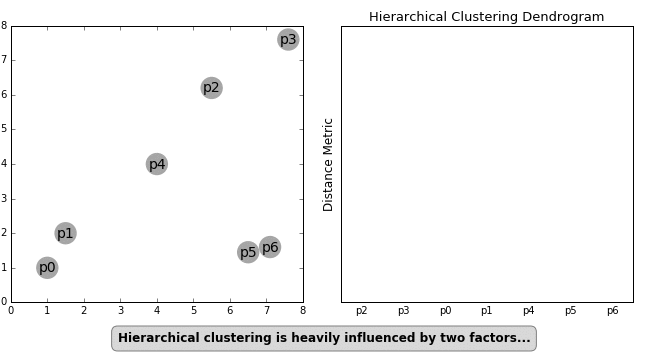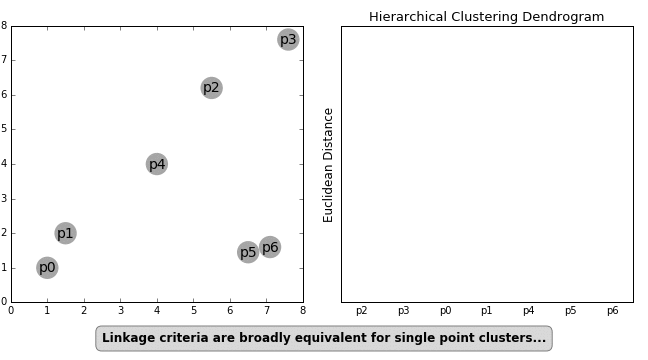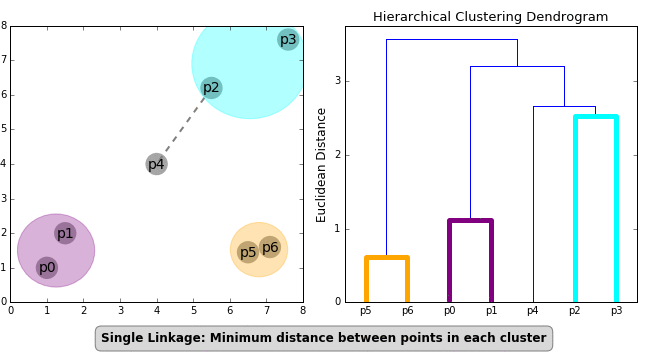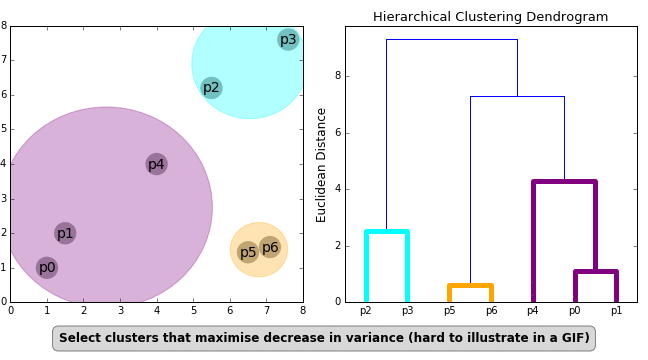
There are three different ways of finding closeness between the clusters :-¶

Closest Pair: Single Linkage Clustering - The distance between any two pairs of clusters is given by the minimum distance between the elements of the pair of the cluster.

\[ d_1(C_i,C_j) = \min _{x \in C_i , y \in C_j}d(x,y) \]

Farthest Pair: Complete Link Clustering - The distance between any two pairs of clusters is given by the maximum distance between the elements of the pair of the cluster.

\[ d_2(C_i,C_j) = \max _{x \in C_i , y \in C_j}d(x,y) \]

Average of all Pairs: Average Link Clustering - The distance between any two pairs of clusters is given by the average distance between the elements of the pair of the cluster.

\[ d_2(C_i,C_j) = avg _{x \in C_i , y \in C_j}d(x,y) \]

Properties Of Single Linkage Algorithm¶

The algorithm can work with any dissimilarity measure, it may not necessarily be metric
There are no Inversions.
- As we run the algorithm (as we start merging the clusters), the dissimilarity scores between merged clusters only increases.

\[ Dissimilarity ~~ at ~~ Level - 2 > Dissimilarity ~~at ~~Level - 5 \]

Objective Function¶

The question that arises while understanding the single linkage algorithm is in terms of it’s objective function.

OR

What kind of clusters is this algorithm trying to create?

To understand this we would need to look up some properties of Single Linkage Clustering

Let’s suppose that we want to create a cluster \( C_1,C_2,....C_k \) which maximizes the inter cluster distance.

\[ maximize~~cost_k(C) \]

\[ cost_k(C)=\min _{C_i,C_j}d(C_i,C_j) \]

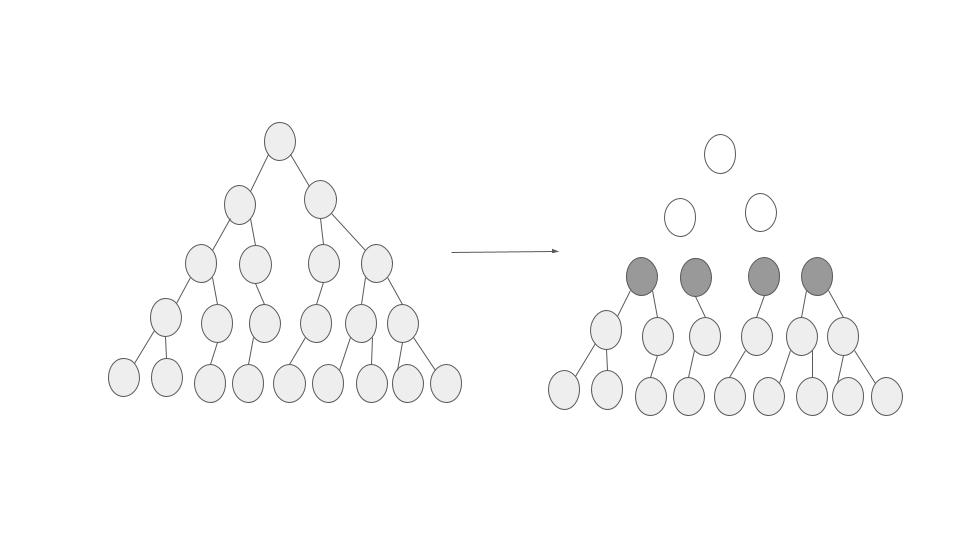
If the above task is our objective function (to maximize the minimum inter cluster distancefor k clusters) then we can easily use single linkage clustering to achieve our objective.

We just have to remove the top k-1 clustering merges and we will achieve k clusters. Also, all these K clusters will follow the above objective function.

CS328-2022 Notes

Hierarchical Clustering

Contents