Expansion and Conductance of a Graph
Contents
Expansion and Conductance of a Graph¶
(1) Expansion of Subset S¶
Let the subset of the graph G be S and \(\overline{S}\) be the complement of the subset S.
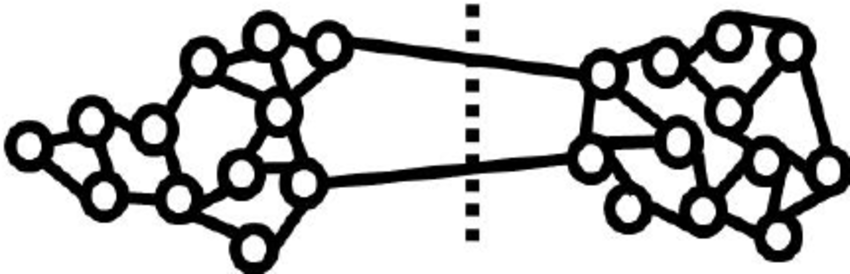
Here S=bhcde and \(\overline{S}\)=agf
\({e(S,\overline{s})} \)=number of edges in between S and \(\overline{S}=\sum_{a\in S,b\in \overline{s}}ab\)
\({|S|}\) =Number of vertices in the subgraph G
In the above example Graph G(V,E):
Here S=bhcde and \(\overline{S}\)=agf
Here \( e(S,\overline{S})\)=3 {ab,gh,fe}
\(min_({|S|},{|\overline{S}|})\)=3
Expansion(S)=3/3=1
Question
Why didn’t we use other forms of denominators?
1) Sum:¶
The denominator results to sum of total vertices and it gives the same result as MIN_CUT.
2)Max:¶
Where n==D(V) , total number of vertices of the graph .
This result is also produce cut similar to Min_cut .
3)Product:¶
This term gives similar result to putting minimum in the denominator.
Note
This above definition was proposed by Computer vision researcher Jitendra Malik and his team.
(2) Conductance¶
It is an indicator of Surface/volume property of graph and we use degree instead of cardinality in the \(Expansion(S,\overline {S})\) as it gives efficient contibution term to the volume aspect of the graph.
Let the subset be of the graph G(V,E) be S and \(\overline{S}\) be the complement of the of subset S.
d(S)= Sum of all degree of vertices in Subset S
\(d(\overline{S})\)=Sum of all degree of vertices in Subset \( \overline{S}\)
Fig. 16 conductance on Graph(G)¶
Here S=bhcde and \(\overline{S}\)=agf
\({e(S,\overline{s})} \)=Number of edges in between S and \(\overline{S}=\sum_{a\in S,b\in \overline{s}}ab \)
\({d(S)}\) =\(\sum_{u\in S}d(u)\) =Degree of the vertices in the subset
In the above example Graph G:
Here S=bhcde and \(\overline{S}\)=agf
Note: For the Regular graph,
For the irregular graphs,conductance term is very crucial as degree caputures the importance|volume property of the graph.
Sparsest Cut¶
For a graph G ,Cut resulting the subset with minimum Conductance\((S,\overline{S})\)
It is also the conductance of Graph G(V,E).
![[Source]](https://upload.wikimedia.org/wikipedia/commons/thumb/8/80/Graph_conductance.svg/330px-Graph_conductance.svg.png){kind=link}
![[Source]](https://www.researchgate.net/profile/Daniel-Simon-11/publication/220910004/figure/fig7/AS:305512227852293@1449851199267/A-sparse-cut-is-a-small-set-of-edges-whose-removal-separates-the-graph-into-two-large.png){kind=link}
Goal
To find the cut with minimum sparsity/conductance.
Min Cut¶
For a graph G,the cut with minimum metric(weights /number of edges) that divides the graph into two disjoint sets.
Definition: A minimum cut S is a partition of the nodes of Graph G into S and \(\overline {S}\) that minimizes the number of edges going across the partition
It is only dependent on the edges and it’s weight between the vertices.
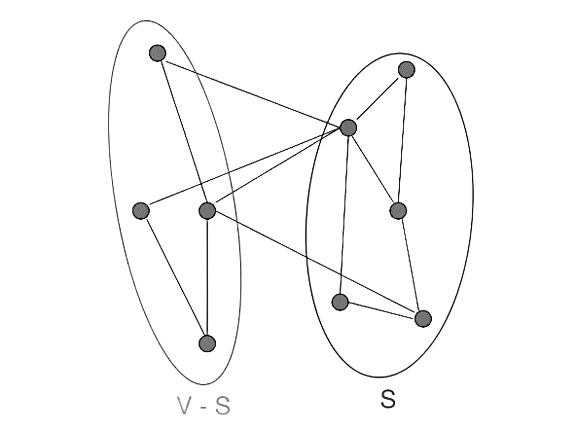
Fig. 18 Min_cut on Graph¶
Illustrations of Min-cut Vs Sparset cut¶
1) K_clique¶
Min Cut:
V(1) and all the other {V(2),V(3),…….V(k)}
\(E(S,\overline{S})\)=k-1 is minimum
Min_cut is isolating one vetex form all other vertices
For this cut conductance(S,\overline{S})=k-1/k_1=1
Fig. 19 Mincut on Kclique¶
Sparsest Cut:
Scenerio:Splitting the graph into equal number vertices
\(E(S,\overline{S})\approx{(k/2)*(k/2))}=\frac{k^2}{4}\)
\(Denomiator=Min_{degree}(S,\overline{S})=(k-1)*(k/2)\)
\(Conductance(S,\overline{S})={\frac{k^2/4}{k*(k-1)/2}}\approx{1/2}\)
This cut is the sparsest cut.
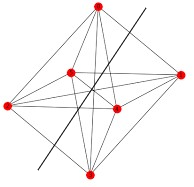
Fig. 20 Sparsecut on Graph¶
2)K_node tree¶
Min Cut:
Scenerio: cut the leaf node.
\(E(S,\overline{S})\)=1 is minimum
Min(degree(S,\overline{S}))=1
conductance(S,|overline{S})=1
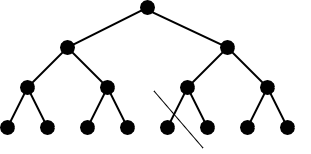
Fig. 21 Mincut on Tree_k¶
Sparsest Cut
Scenerio:cut the first child of root node apart.
\(E(S,\overline{S})\)=1
\(Mindegree(S,\overline{S})\)=2(|s|-1)
\(conductance(S,\overline{S})=\frac{1}{2|S|-1}\)
assuming \( |S|\leq|\overline{S}|\leq{k/2}\)
To minimise the conductance we need to maximise the denominator
\( |S|\to{k/2}\)
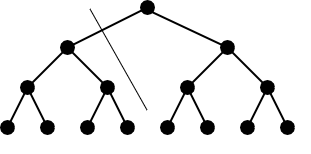
Fig. 22 Sparse Cut on Tree_K¶
This cut is the sparsest cut.
3)K_clique combination¶
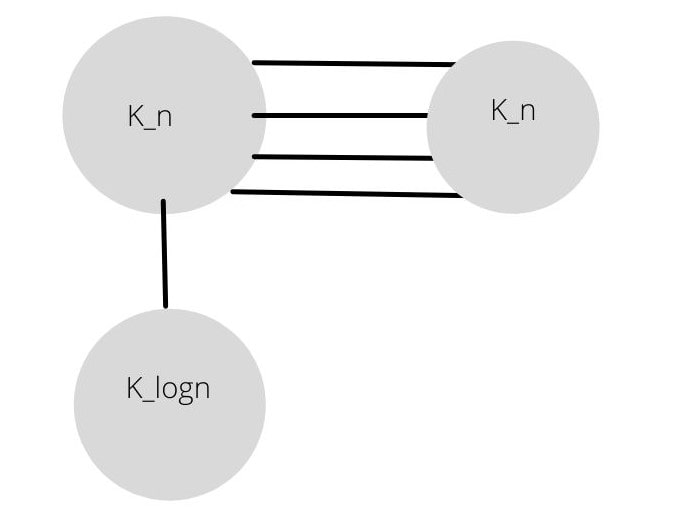
Fig. 23 kclique_combination¶
Here, there n edges matched between two K_n graphs and one edge between K_n and K_logn.
Min Cut:
Scenerio: cut the edge between k_n and K_logn.
\(E(S,\overline{S})\)=1 is minimum
\(Min(degree(S,\overline{S}))=\theta{(log(n)^2)}\), k_logn is a clique
\(conductance(S,\overline{S})\approx{\frac{1}{\theta{(log(n)^2})}}\)
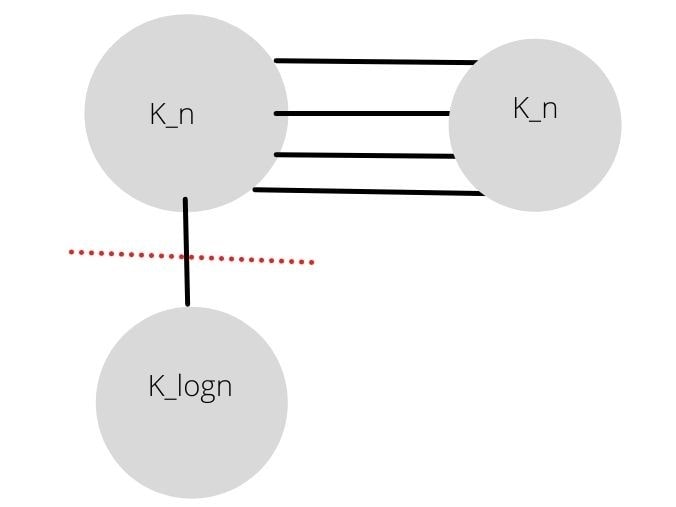
Fig. 24 k_n_Min cut¶
Sparsest Cut
Scenerio:cut the edges between the K_n and K_n
\(E(S,\overline{S})\)=n
\(Mindegree(S,\overline{S})\approx{\theta{(n^2)}}\), assuming k_n is a clique
\(conductance(S,\overline{S})\approx{\frac{n}{\theta{(n^2)}}}\)
To minimise the conductance we need to maximise the denominator
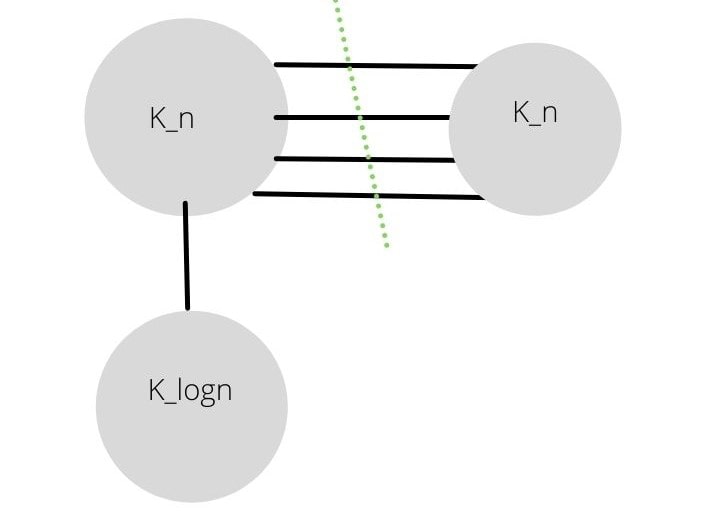
Fig. 25 k_n_Sparsest Cut¶
This cut is the sparsest cut.
Note
(1) These edges in a graph gives the interaction between the node/data.
(2) Clustering is grouping of nodes which are more connceted than others.This Conductance calculation results in fraction of edges that goes from from one cluster set(S) to the S compliment.
(3) Higher the conductance implies harder to disconnet the graph G into parts.
We can apply this conductance concept to solve some classic problems like Randoom walks,divide and conquer algorithms,finding communities in social networks,various network design problems e.t.c.
References:
Here are the sources for images [Sparsest Cut] and [Expansion on Graph(G)]