.ipynb .pdf

repository open issue suggest edit

Binder Colab Live Code

Contents

Mixture Models

• Data is assumed to come from one of many distributions

*\(D_{1}\)(x), \(D_{2}\)(x) …\(D_{k}\)(x) - the k difference distributions *Each data point is picked from one of these

Motivation:

Formalizing the data generative model and coming up with principled soft/hard clustering algorithms

#General Mixture Model

• Model can be “hard” (each point from single cluster), or “soft” (each point belongs to multiple clusters)

• Appropriateness depends on context

• Captures difference between hard and soft clustering

• Prominent examples

• Gaussian mixture

• Topic models for documents

Applications for mixture models

• Formalization of clustering - allows us to view clustering as a real parameter estimation problem, and thereby derive the clustering definition

• Often, even when data is not cleanly clusterable, can fit a mixture to estimate different parameters of subgroups

Example 1 - house price modelling

• Data - prices of N houses

• House price depends on various factors

• Generative model

• Price = function(neighborhood, area, design)+noise

Example 2 - topics in a document

• Data = set of documents

• document = bag of words

• Topic = a probability distribution over vocabulary

• Generative model

• Choose a topic at random

• Choose words for that topic

Example 3 - handwriting recognition

• Data = 64 x 64 images, each of one handwritten digit

• Generative model = pixel intensities from ideal digit + noise

• Each mixture component =

(fix an “ideal” way of writing a digit) + noise

• \( D_{1}(x) = μ_{1} + noise \) intensities that come from “ideal 9” query handwritten digit

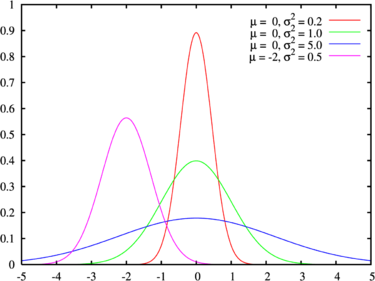
Fig. 30 Here is my figure caption!

#Gaussian Mixture Model

Each data point is generated first by choosing the particular Gaussian and then generating a sample from it

Note

Given the points, can we learn all the parameters, including the correct label of every point?

• D_{i}(x) = N(μ_{i}, σ^2_{i}), i = 1,2,…..,

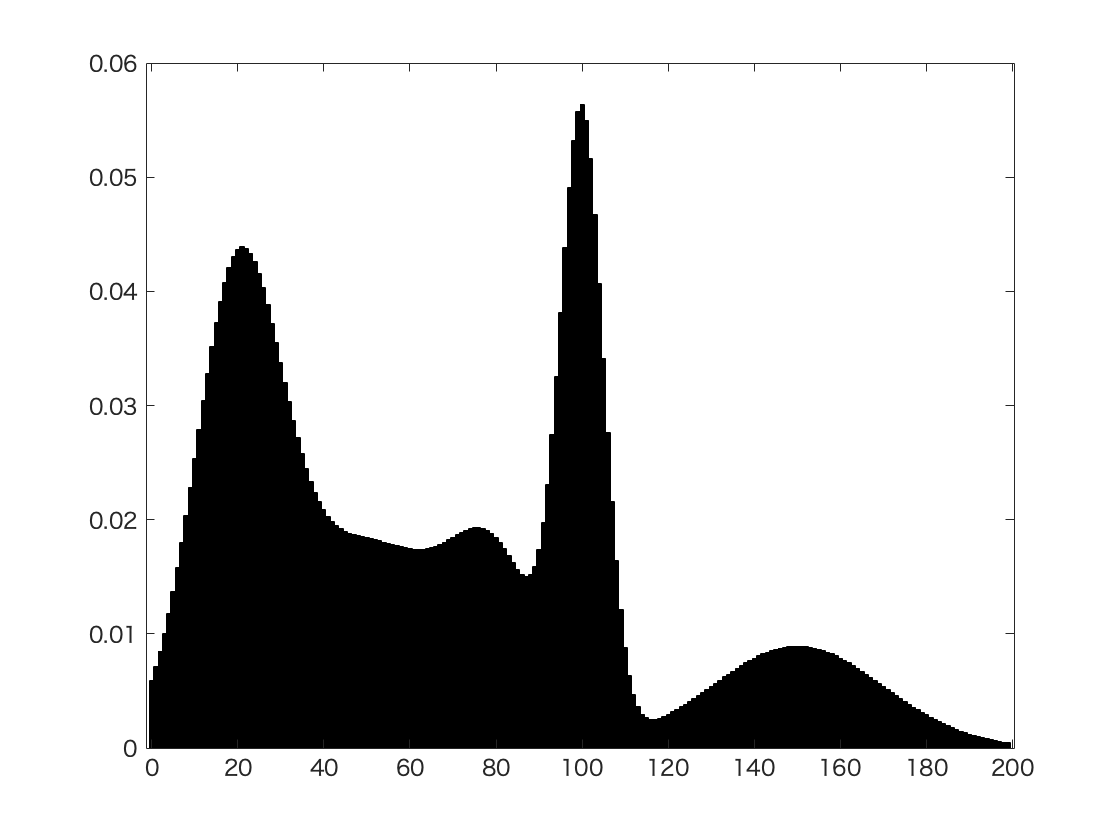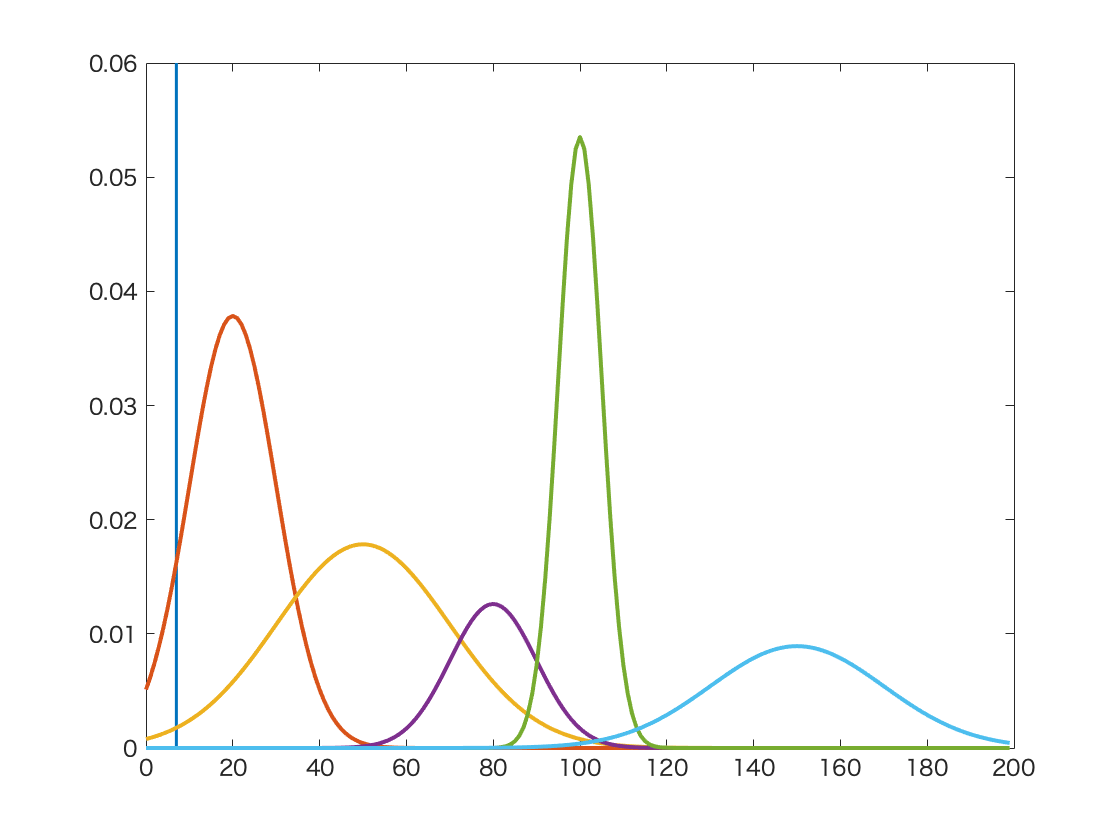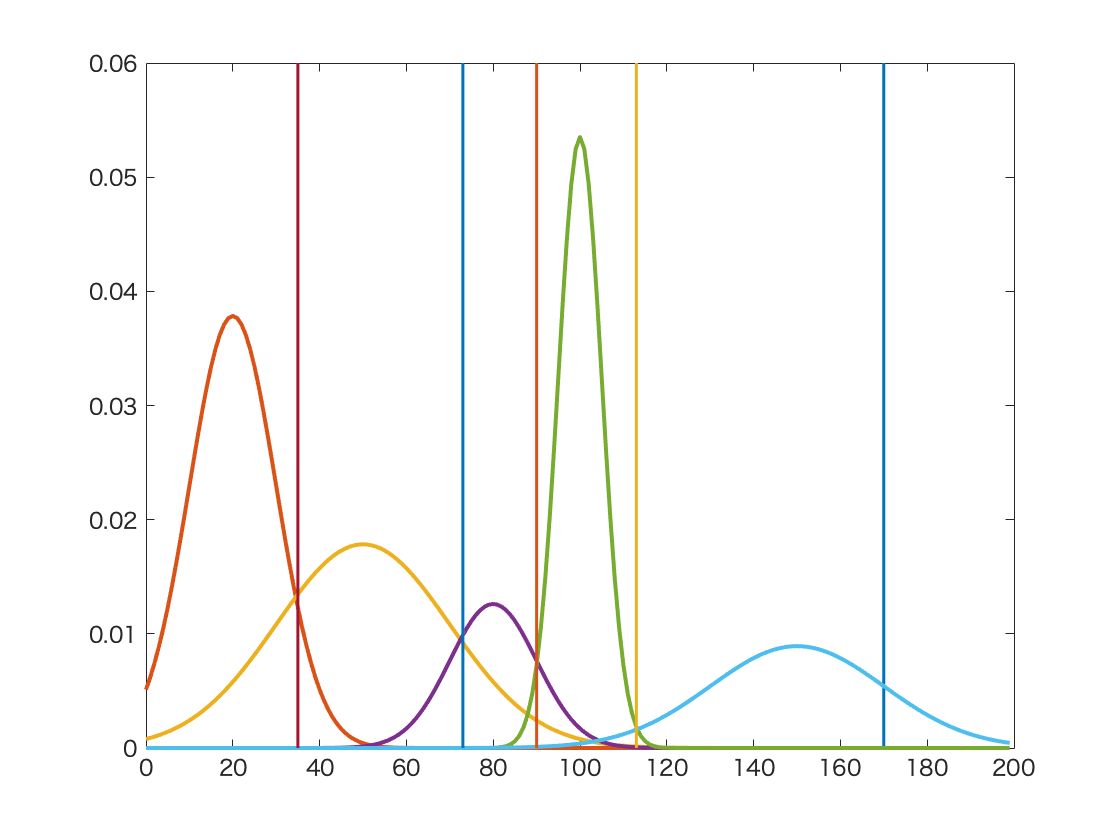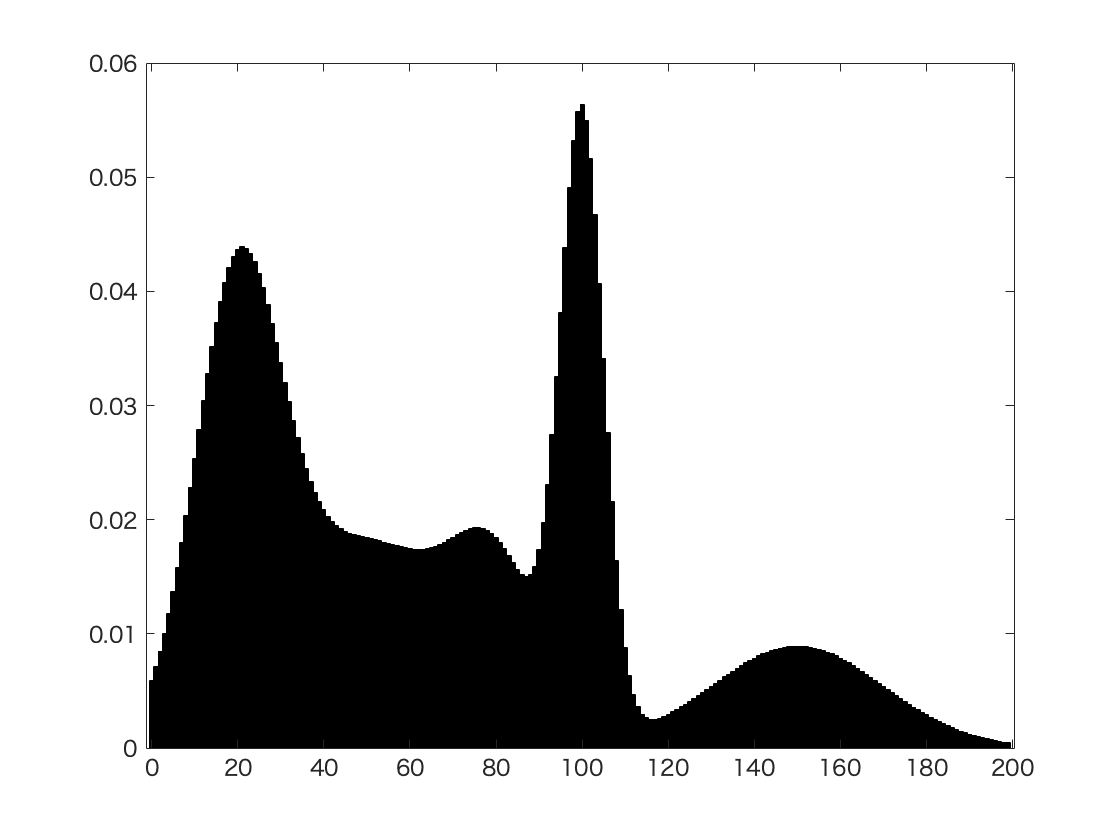
Fig. 31 An example of Gaussian Mixture in image segmentation with grey histogram

Each data point is generated in the following manner:

• Toss a k-faced dice, where probability of i^th face = \(W_{i}\)

• If face j appears, then generate a point by sampling from \( D_{i}(x) = N(μ_{i},σ^2_{i}) \)

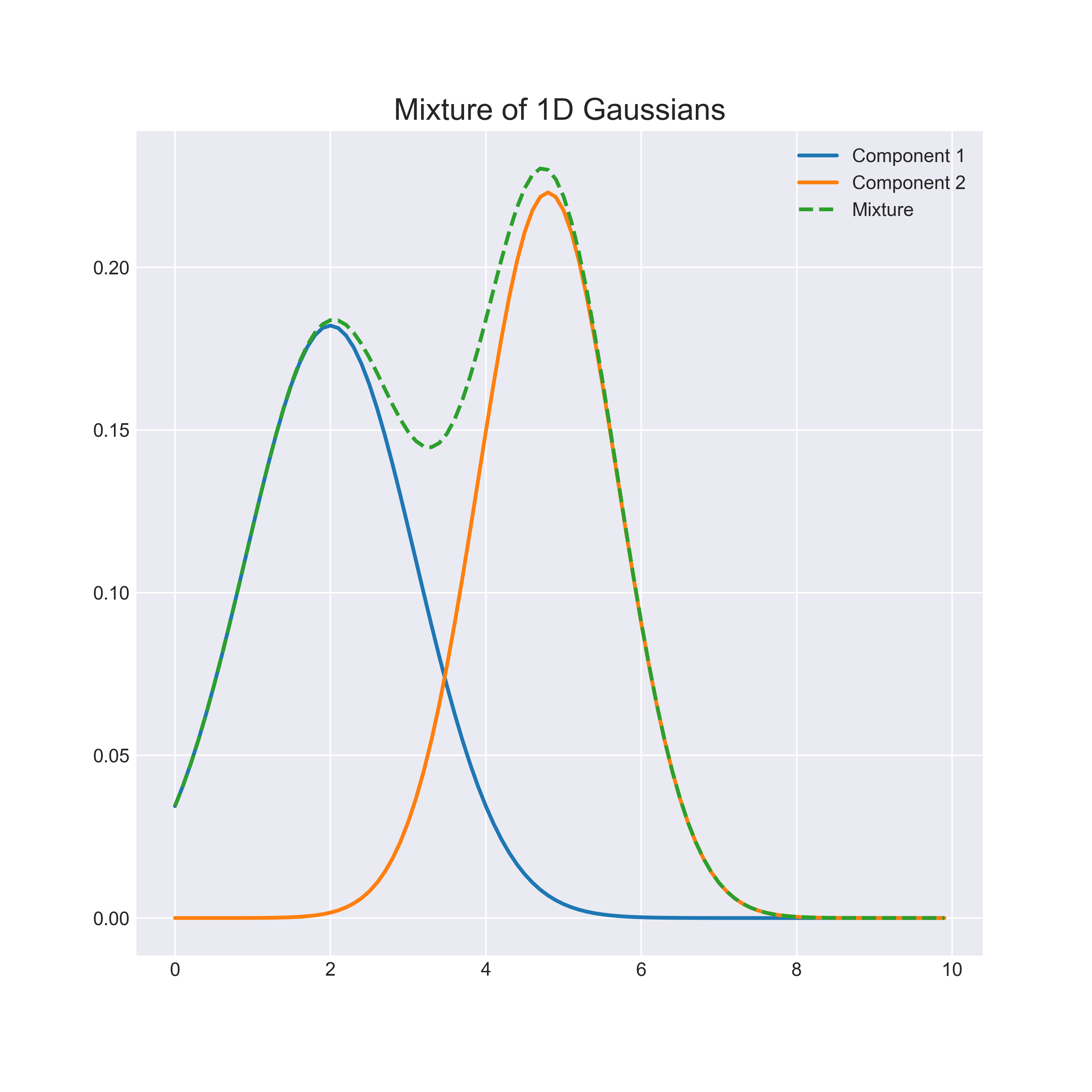
Fig. 32 This is an example of guassian mixture model with 2 componenets

Given the points only can we learn all the parameters, including the correct label of every point

Combined pdf = \( \Sigma _{i≤n} w_{i}N(μ_{i},σ^2_{i}) \)

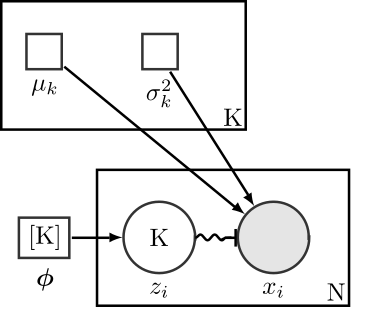
Fig. 33 Here is my figure caption!

Note

Bayesian Gaussian mixture model using plate notation.

Fig. 34 Here is my figure caption!

Observation

For the Gaussian mixture model, the pdf is \( \Sigma _{i≤n} w_{i}N(μ_{i},σ^2_{i}) \)

Is this the same as pdf to \( w_{1}Z_{1} + ... w_{k}Z_{k}, where \) \( Z_{i}~N(μ_{i},σ^2_{i})? \)

#Bit of history!

• Originally proposed in 1894, Karl Pearson, to classify crab population

• Proposed a “method of moments”, required solving a 9th degree polynomial to find the roots!

• Subsequent research yielded more efficient algorithm, under certain assumptions

previous

Relation between second eigenvalue of Laplacian and Spectral Clustering

next

Gaussian Annulus Theorem