Markov and Chebyshev Inequalities¶

Markov Inequality¶

Let \(X\) be a non-negative random variable and \(a>0\) then the probablity that \(X\) is atleast \(a\) is less than equal to the Expectation of \(X\) divided by \(a\):

\[P(X \geqslant a) \leqslant \frac{E[X]}{a} \hspace{0.5cm} \text { For any } a>0\]

Proof. Consider

\[ E(X)=\int_{0}^{\infty} x p(x) d x \]

\[ E(X)=\int_{0}^{a} x p(x) d x+\int_{a}^{\infty} x p(x) d x \]

\[ \geq \int_{a}^{\infty} x p(x) d x \]

\[ \geq \int_{a}^{\infty} a p(x) d \]

\[ = a \int_{a}^{\infty} p(x) = a P[X \geq a] dx \]

\[ E(X) \geq a P[X \geq a] \]

\[ \therefore P(X \geqslant a) \leqslant \frac{E[X]}{a} \]

Tip

Markov’s inequality is not useful when \( a < E(x) \)

Chebyshev’s Inequality¶

Motivation:¶

Markov’s inequality does not consider left hand side of expectation ( \(\mu\)) and hence does not give any information on its distribution.

In case of a in left hand side of \( \mu \) ,therefore for all \(X\), \(\frac{\operatorname{E}[X]}{a} \leq 1 \)

\[ \operatorname{Pr}(X \geq a) \leq \frac{\operatorname{E}[X]}{a} \]

This statement is not at all useful as it implies that the probability of the said event is less than 1 which is trivial.
So we want to define a bound on the probability, that X takes values large than expectation by a ( \(\mu + a\) ) and smaller than expectation by a ( \( \mu - a \) ).
Chebyshev’s inequality is a better version /improvement on Markov’s inequality.

Chebyshev’s inequality is given as:¶

\[ \operatorname{Pr}(|X-\mathbf{E}[X]| \geq a) \leq \frac{\operatorname{Var}[X]}{a^{2}} \]

We can analytically verify that on increasing \(\sigma\), probability of \(|X-\mathbf{E}[X]| \geq a\) increase as distribution spread out. Also, with an increase in \(a\), it is less probable to find \(X\) in that interval.

Proof. In markov’s inequality \(Y\) is non negative similarly, \( Y^{2}\) is also non negative.

\[\begin{split} \begin{array}{l} Y=X-E[X] \\ Y^{2}=\left(X-E[X )^{2} \quad\right. \\ P\left[Y^{2} \geqslant a^{2}\right] \leq \left .\frac{\sigma^{2}}{a^{2}}\right. \\ \text { where } \quad \sigma^{2}=E\left[Y^{2}\right] \end{array} \end{split}\]

We can say that

\[ \operatorname{Pr}(|X-\mathbf{E}[X]| \geq a)=\operatorname{Pr}\left((X-\mathbf{E}[X])^{2} \geq a^{2}\right) \]

Hence

\[ \operatorname{Pr}\left((X-\mathbf{E}[X])^{2} \geq a^{2}\right) \leq \frac{\mathbf{E}\left[(X-\mathbf{E}[X])^{2}\right]}{a^{2}}=\frac{\operatorname{Var}[X]}{a^{2}} \]

How do we visualize Markov’s Inequality and Chebyshev’s inequality?¶

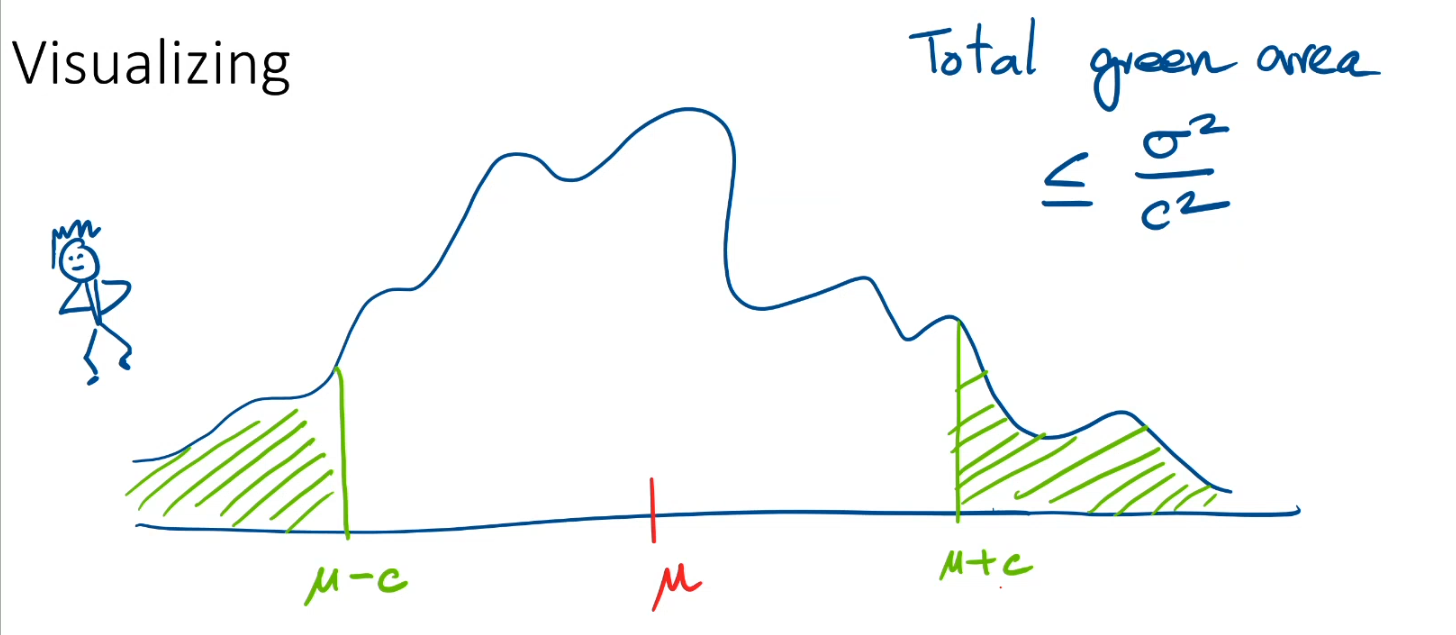
Fig. 10 A Schematic of region bounded by chebyshev inequality¶

The area of left green shaded interval is less than \(\frac{\mu}{\mu +c}\)
The area of the toatal green-shaded interval is less than \(\frac{\operatorname{Var}[X]}{a^{2}}\) .
Typically Chebyshev’s inequality is stronger than Markov’s, but we can not say that in general, its true. In certain conditions, the reverse is true.

Moment Genrating Functions¶

In proof we saw that \((X-\mathbf{E}[X])^{2}\) is better than \((X-\mathbf{E}[X])\)

What is so special about working with \(X^{2}\) and why not other functions?

Moment generating functions of \(X\) are stronger bound than \(X^{2}\)

For a random variable \(X\), let \( Y = \text{exp}(tX) \) for some \(t \in \mathbb{R} \) . The moment generating function of \(X\) is defined as expectation of \(Y\).

\[E[e^{tX}] = 1 + tE[X] + \frac{t^2}{2!}E[X^2] + ... + \frac{t^{k}}{k!}E[X^{k}]\]

Let us take the second derivative of \(E[e^{tX}]\) with respect to \(t\) at \(t=0\),

\[\Big(\frac{d^2}{dt^2}(E[e^{tX}])\Big)_{t=0} = E[X^2] \]

Similarly taking the \(k\)-th derivative of the moment generating function with \(t=0\), we can get the \(k\)-th moment of \(X\).

CS328-2022 Notes

Markov and Chebyshev Inequalities

Contents