Why does k-means++ work?¶

Consider a cluster C that OPT uses. If we select a point from there then that cluster is covered “pretty well”.
- cost incurred by our center is with some constant * cost incurred by OPT.
If we select two points from the same OPT cluster, it must be because the contribution of other clusters to the OPT cost is small.

Parallelizing K-means¶

Suppose the data is distributed on multiple machines.
So can we parallelize K-means??
Partition the data,
- Let \(X_1, X_2, .... , X_p\) be the partitions.
In parallel compute a clustering for each \(X_i\)
- \(C_1^i,....,C_k^i\) be the clustering, define \(W_i^j = |C_i^j|\)
Consider the cluster centroids as points with weights \(W_i^j\) and then recluster them.

Note

The weight is equal to number of points associated with the center \(C_i\) in a cluster.

Example¶

Let there are four machines and we want to run k-means algorithm.
Therefore, we let each machine run k-means on their data set and come up with k centers. (Phase 1)
we will assign these k centers their weight which will be equal to the number of points associated with that particular center.
Therefore, we have 4k centers and now we can shift these to one center cluster and run k means algorithm on these 4k points. (Phase 2)

So how good is the solution?¶

Suppose the algorithm in phase 1 gave a \(\beta\) approximation solution and the algorithm in phase 2 gave \(\gamma\) approximation solution.
Theorem (GNMO00, AJM09): Overall we get a 4\(\gamma(1+\beta)\) + 2\(\beta\) approx.
Setting \(\beta = \gamma\) = O(logk) would give a O\((log^2k)\) approx.

Hierarchical clustering¶

k-means/K-median worked on the intuition that clusters are “balls” in high dimension.
Also we have to know the number of centers we are working with.
So what can we do when we do not know the target number of clusters?
can we produce a family of clustering, for each k?
There are two ways-

Top-down/divisive: Keep on creating bi-partition (applying 2-means)
Bottom-up/agglomerative: start from individual point and keep on aggregating.

Divisive clustering¶

This is a top-down clustering approach, initially all the data points belong to one cluster and then keep on creating bi-partition recursively (applying 2-means)

Agglomerative clustering¶

This is bottom-up clustering approach, initially each data point is a cluster of its own, then keep on merging closest set of data points to build larger clusters from smaller ones.

Algo:

- keep a current list of clusters
- Initially, each point in its own cluster
- while #clusters>1:
    - choose closest pair
    - merge them,
    - update list by deleting these and adding new cluster.

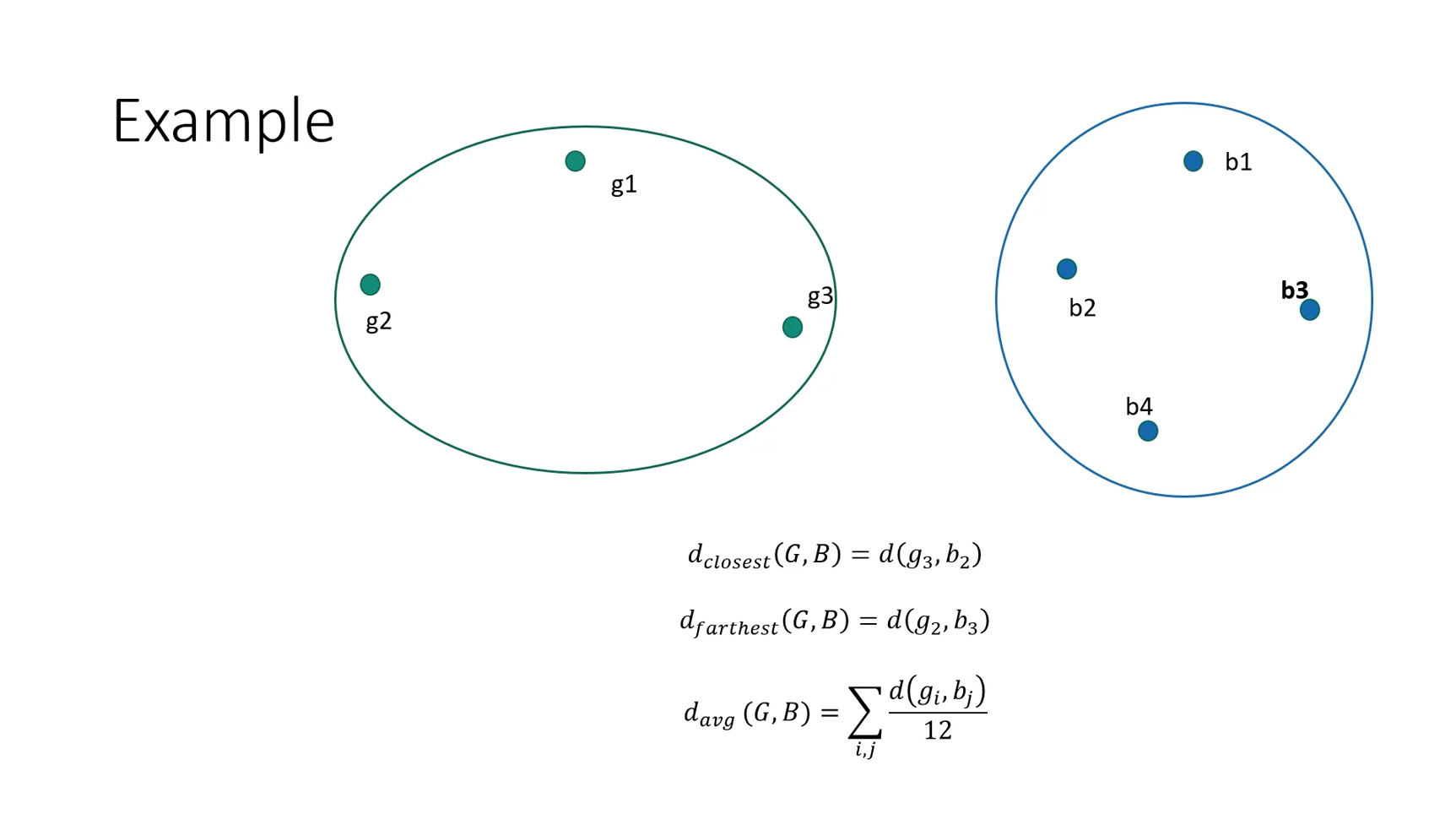
But how do we define closest pair or the closeness between two clusters?

There can be many ways, some of them are-

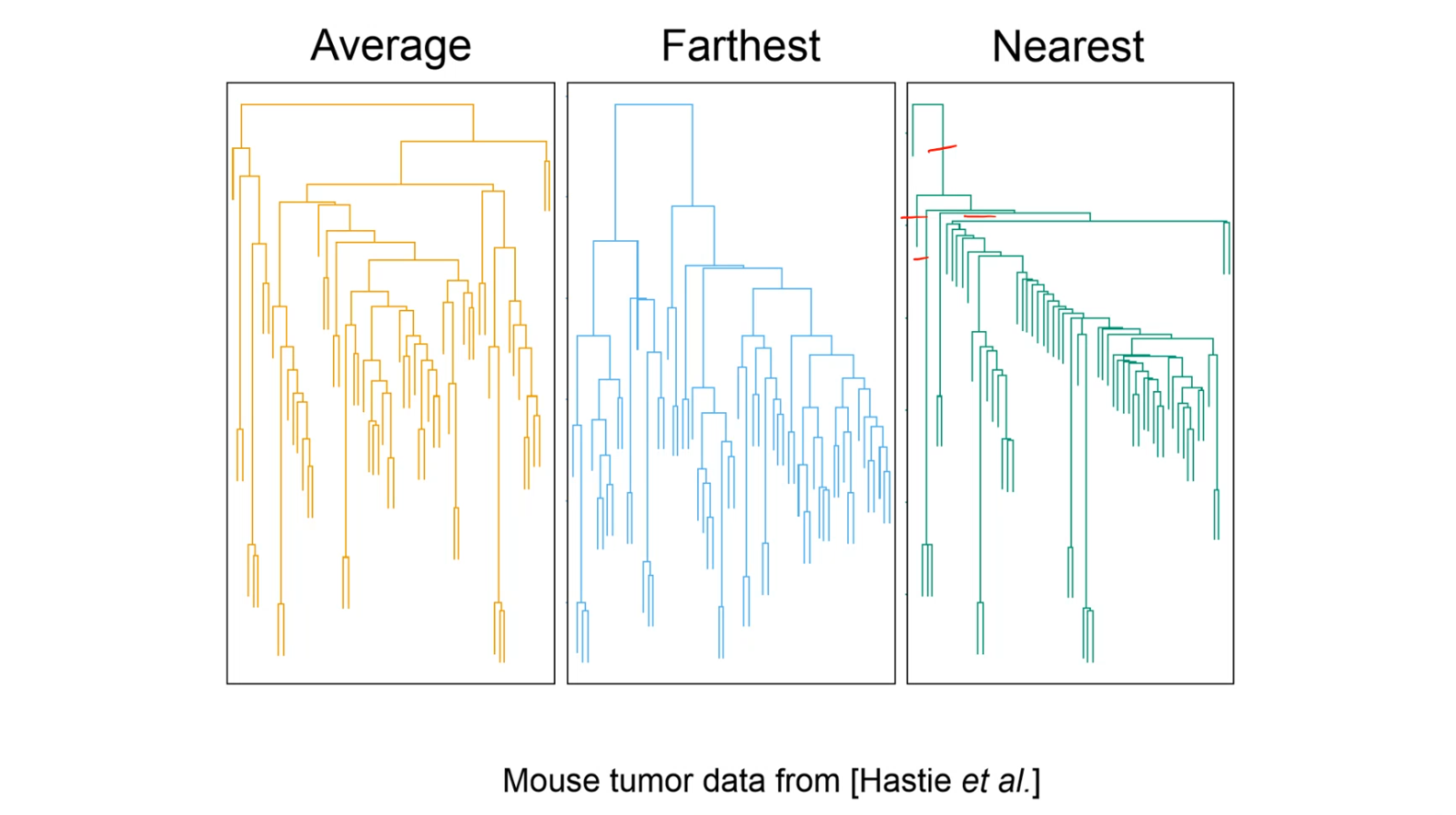
Closest pair: single linkage clustering -> \(d_1\)(C,C’) = \(\underset{x \epsilon C,y \epsilon C'}{min}\) d(x,y)
Furthest pair: complete link clustering -> \(d_2\)(C,C’) = \(\underset{x \epsilon C,y \epsilon C'}{max}\) d(x,y)
Average of all pairs: average link -> \(d_3\)(C,C’) = \(\underset{x \epsilon C,y \epsilon C'}{avg}\) d(x,y)

Note

All the images are taken from the slides provided by the Prof. Anirban Dasgupta.

CS328-2022 Notes

Why does k-means++ work?

Contents