Streaming Models and Answering Inclusion Queries¶

Stream sampling is a process of collecting a representative sample of the elements of a data stream.The sample is usually much smaller than the entire stream, but can be designed to retain many important characteristics of the stream, and can be used to estimate many important aggregates on the stream.

In this section, we are going to learn about memory efficent computing when the space is at crunch. We are assuming two important assumptions in this section.

data arrives in a stream or streams and if it is not processed or stored, then it is lost forever.
data arrives so rapidly that it is not feasible to store it and then interact with it at the time of our choosing.

Examples of the streaming data

Sensor data: Imagine a temperature sensor above the ocean, sending information about the surface temperature to the base station at every hour.
Image data: Sateliites often send infromation to the earth which consists of terabytes of the information.
Internet and Web Traffic

Remark

Streams often deliver elements very rapidly. We must process them quickly otherwise we may lose the opportunity to process them at all. Thus it is important that the streaming algortihm is executed in the main memory with rare accessing the secondary memory.
Even if the stream requires only small portion of main memory for the computation, the requirements of all streams together can exceed the main memory.

Sampling Data in a Stream¶

Suppose we have \(a_1\), \(a_2\), \(a_3\), …… \(a_n\) distinct items in a stream belongs to some universe U. Our goal is to sample a set S from the stream such that \(|\)S\(|\) \(=\) \(k\) and p[x \(\in\) S] = \(\frac kn\) \(\forall\)\(x\) in the stream.

There are two cases possible while sampling from the stream based on the length of the stream.

Case1 : We know the length of stream is known and finite.

Can choose k random positions out of n and use the entries in those positions
The samples are obtained only after reading through the entire stream

Case2 : We don’t know the length of the stream i.e; n is unknown or n is infinite.

We can use Reservoir Sampling

Reservoir Sampling¶

Assume we are sampling only single item then k=1. Suppose we have \(a_1\), \(a_2\), \(a_3\), …\(a_i\)… \(a_n\) distinct items in a stream belongs to some universe U where we don’t know n in advance. then

\[ pr[a_i \ is \ chosen] = \frac 1n \]

Since k=1 we will have a one memory cell to store one sample from the data. Let that memeory cell be s.

Now the probability of \(a_i\) replacing the element previously in the memory cell is \(\frac 1i\) and move on is \(1 - \frac1i\).

Now let us suppose the ith item is in the final stored in the memory cell.

\[pr[s = a_i] = \frac 1i \times(1-\frac1{i+1})\times(1-\frac 1{i+2})\times.......\times(1-\frac 1n)\]

since ith element must be chosen and (i+1)th, (i+2)th…nth elements must move on.

Hence,

\[pr[s = a_i] = \frac 1i \times(\frac{i}{i+1})\times(\frac{i+1}{i+2})\times ....... \times\frac{n-1}n) pr[s = a_i] = \frac 1n\]

With this information, now let us solve for the case any k.

Suppose if we want to make sampling k items with replacement of items then do k parallel independent reservoir sampling for single items. Suppose if we want to make sampling k items without replacement of items. This time we are going to have k memory cells. Follow the below algortihm:

for the first k items in the stream simply assign them to the k memory cells.

for (i>k):

       j = random number from 1,2,3,4...i
       if(j<=k):
           replace jth memory cell with ith element

Now let us suppose the ith item is the occured in the chosen subset.

\[pr[a_i \in S] = \frac ki \times(1-\frac1{i+1})\times(1-\frac 1{i+2})\times .......\times(1-\frac 1n)\]

since ith element must be chosen and placed in one of the k cells and (i+1)th, (i+2)th…nth elements should not fall on that location.

Hence,

\[pr[a_i \in S] = \frac ki \times(\frac{i}{i+1})\times(\frac{i+1}{i+2})\times ....... \times\frac{n-1}n) \]

\[pr[a_i \in S] = \frac kn \]

Here reservoir is analogus to memeory cell. At at every step i, all items from 1,2,3,..\(i\) will have the same probability \(\frac1i\) being in the reservoir.

Hashing¶

Elements come from universe U, but we need to store only only n items where n<\(|\)U\(|\).

In hash table, we will have an array size m and hash function ‘h’ that maps elements from Universe to the set {0,1,2,..m-1}. We typically use \(m ≪ |U|\) and \(m < n\)

Collisions happen when \(x ≠ y\), but \(h (x) = h(y)\)

In theory, we design for worst-case behaviour of data. So, We Need to choose hash function “randomly”.

Suppose there is a Hash family H = {\(h_1, h_2, ... \)}. When creating a hash table, we choose a random hash function and start analysing the expected query time. However, the algorithm has to carry around the “description” of the hash function, it needs log(\(|H|\)) bits of storage.

Warning

\(|H|\) cannot be too big, in particular, it cannot be the set \([m]^U\), all possible functions

Hash Family¶

We need to define a way to create a hash function that requires only small amount of “parameter storage”. We can also look it as follows: Suppose we have a set of parameters \(a_1\), \(a_2\), \(a_3\), …. \(a_k\). Setting these parameters randomly defines the hash function. It is also important to create small hash families H such that choosing from it gives a function with “good behaviour”. Here are some hash families.

\[Uniform \ : \ Pr_{h \in H}[h(x) = i] = \frac{1}{m} \ \ \forall x,i\]

\[Universal \ : \ Pr_{h}[h(x) = h(y)] = \frac{1}{m} \ \ \forall x\neq y \]

\[Near \ Universal \ : \ Pr_{h}[h(x) = h(y)] \leq \frac{2}{m} \ \ \forall x\neq y \]

Chaining¶

When we are trying to insert items based on the hash values, if two items get the same hash values, we say that the two items are colliding. When collisons happen, we store that elements in that hash value using linked lists.

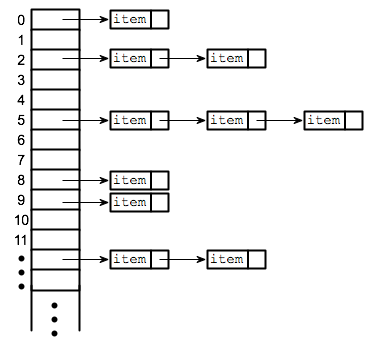
Fig. 36 Hash table¶

Suppose l(x) = length of the chain at position h(x). Expected time to query x = \(O(1 + E_h[l(x)])\). It is same for insert and delete.

Now let us define

\[\begin{split} for \ \ x\neq y \ \ C_{xy}= \left\{ \begin{array}{ll} 1 & if \ \ h(x) = h(y)\\ 0 & else\\ \end{array} \right. \end{split}\]

\[E_{h}[l(x)] = E_{h}[\sum_{y}C_{xy}]\]

For universal hashing

\[E_{h}[l(x)] = E_{h}[\sum_{y}C_{xy}] = \sum_{y}E_{h}[p(x) = p(y)] = \frac nm\]

Prime Multiplicative Hashing¶

Prime Multiplicative hashing is used to design small and universal hash family.

Fix a prime number p > \(|U|\)
H = {\(h_a\) (x) = ((ax + b)mod p)mod m, a, b ∈ {1, … p − 1 }}
Choosing a hash function is same as choosing a, b ∈ {1, … p − 1}.

CS328-2022 Notes

Streaming Models and Answering Inclusion Queries

Contents