Densest Subgraphs¶

Density of Subgraph¶

Density of a subgraph
- Density measures how tightly the components inside a subgraph are connected to each other.
- It does not care about the connectivity with the components outside the subgraph.
Mathematically, Density of a subgraph is represented by the following formula:

\[ D(S) = \frac{e(S,S)}{|S|} ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ - (1)\]
- e(S,S) is the number of edges between nodes both in S or e(S,S) = { ( x , y ) \(\in\) E ; x \(\in\) S, y \(\in\) S }
- |S| is the number of nodes in subgraph S.
Significance of |S|
- Simply calculating e(S,S) won’t be enough to determine how tighty the components are connected. For eg, in the figure shown below e(S,S) of Subgraph A is more however we can easily notice that subgraph B is more dense.
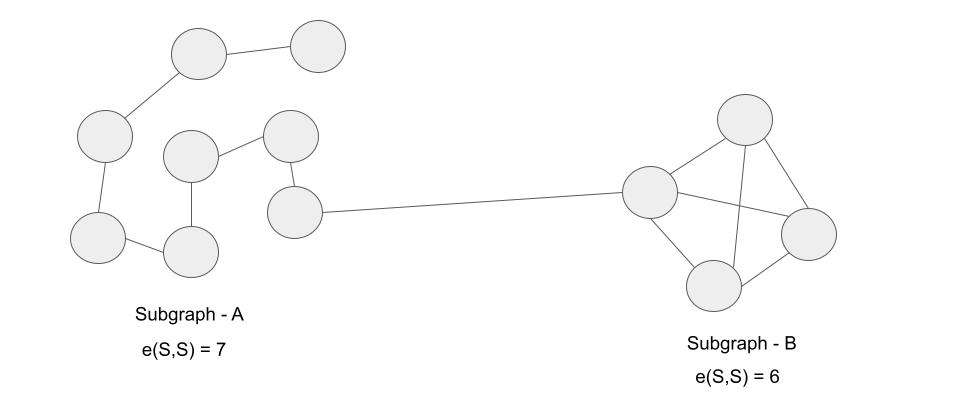\[ Figure - 1 \]
- We can’t consider denominator as \({|S|}^{2}\) as \( \max\limits_{S} \frac{e(S,S)}{{|S|}^{2}} \) is trivial, irrespective of the nature of graph.
- However \( \max\limits_{S} \ \frac{e(S,S)}{|S|} \) is non-trivial for different types of graphs.

Note

(|S|)(|S|-1) can’t be considered as denominator (as it becomes zero for |S| = 1) even though it gives a tight upper bound on Density of Subgraph.

Let us assume the Density of a Subgraph \(\ge\) a constant (say \(\frac{c}{2}\))
\( \therefore \frac{e(S,S)}{|S|} \ge \frac{c}{2}\)
On Rearranging, \( 2e(S,S) \ge c|S|\)
\(\because 2e(S,S) = deg(S) - e(S,\overline{S}) \) , \( deg(S) + e(S,\overline{S}) \ge c|S|\)
\( deg(S) + deg(\overline{S}) - deg(\overline{S}) - e(S,\overline{S}) \ge c|S| \)
We know that, \( deg(S) + deg(\overline{S}) = 2|E|\)
\( \therefore 2|E| \ge c|S| + deg(\overline{S}) + e(S,\overline{S})\) - (2)

Maximum Flow or Min-cut algorithm is an algorithm that gives us the maximum feasible flow through a network or the minimum cuts required to stop the flow through the network.
We can find the densest subgraph by using a Decision problem where we need to find if there exist any subgraph S with density more than a fixed value let’s say \( \frac{c}{2}\).
Then using binary search it finds the maximum value of c for which there exists a subgraph such that \( \frac{e(S,S)}{|S|}=\frac{c}{2} \)
Max Flow Algorithm :-
- Binary search on value of c
  - Let the original graph be G.
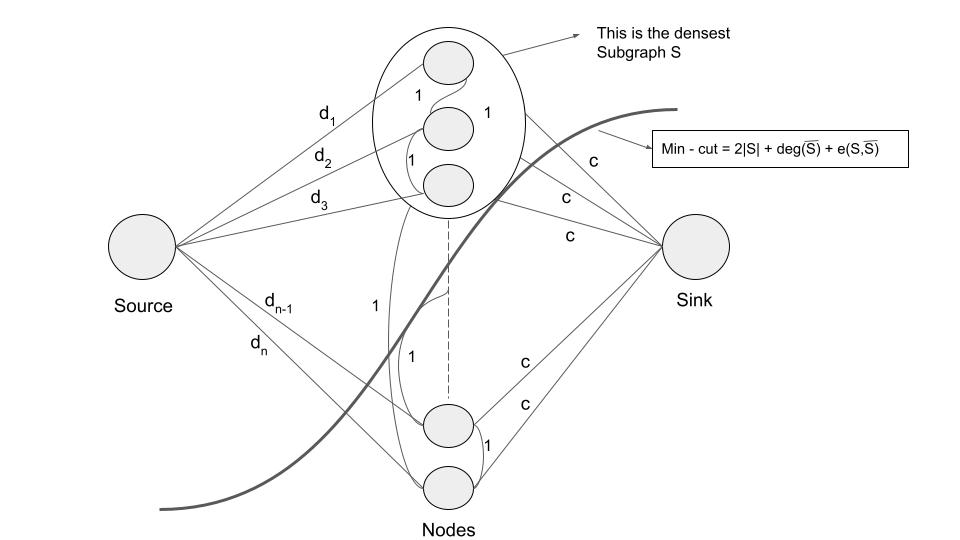
  - Now let us construct a new graph G’ such that it has 2 extra nodes than G (Source and Sink).
  - Connect all the nodes (undirected) in G to the source and assign weight of each edge as the degree of the node. For eg, if degree of node \(\nu\) is \( {d}_{i} \) then assign weight of edge from source to \(\nu\) as \( {d}_{i} \).
  - Connect all the nodes to sink and assign weight of all the edges as c.
  - Run the max flow algorithm (Ford-Fulkerson).
  - It will always return a cut \(\le 2|E|\) .
  - Assign Densest Subgraph as S (Shown in the figure).
  - Repeat all the steps with new value of c as per binary search.
The runtime of this algorithm in O(log(C) \({|E|}^{2}\) U), where U is the value of maximum flow.

\[ Figure - 2 \]

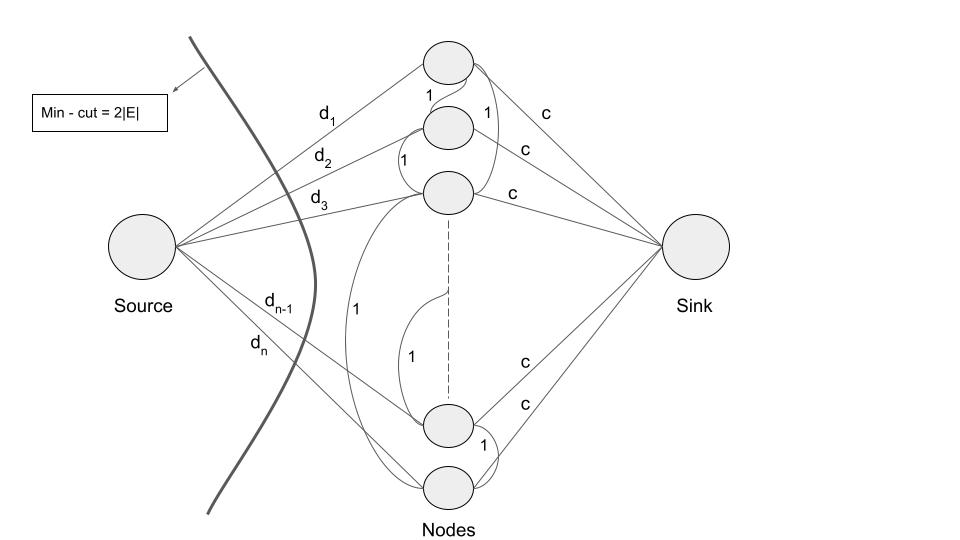
As you can see in the Figure - 2 that the min cut will atmost be 2|E| and we can always have a cut of less than 2|E|.
In this type of cut there is no densest graph since there are no nodes to the left of the cut.

\[ Figure - 3 \]

In Figure - 3, we can see that there is a subset of nodes which is to the left of min-cut.
This Subset satisfies the condition given by the right hand side of the equation \( 2|E| \ge c|S| + deg(\overline{S}) + e(S,\overline{S})\).
Hence for maximum value of c, this is the desired densest subgraph.